8.1. Arrays Basics#
NumPy arrays (n-dimensional array, or ndarray) are like a super-powered list that can store numbers in rows and columns. You will learn that some array operations are similar, if not the same, as Python lists.
NumPy arrays essentially come in two flavors, vectors and matrices:
Vectors are strictly 1-d arrays that have only one axis, and
Matrices are 2-d arrays with two axes: (rows, columns).
Here in this section, we discuss topics regarding NumPy arrays:
creation
indexing/slicing
general array attributes and functions such as ndim, dtype, shape, reshape()
8.1.1. NumPy Environment#
8.1.1.1. Data Structure#
The primary data structure in NumPy is the N-dimensional array, or ndarray. NumPy’s arrays are a list of lists in Python, but are more compact than Python lists. In essence, a Python list is an array of pointers to heterogeneous Python objects, while a NumPy array is an array of uniform values of the same type (e.g., all integers, all floats) and array elements are stored in one continuous block of memory, similar to how arrays work in C (Fig. 8.1). Python lists are more flexible, but Numpy arrays are smaller in file size, and access in reading and writing items is much faster [Martelli, 2009].
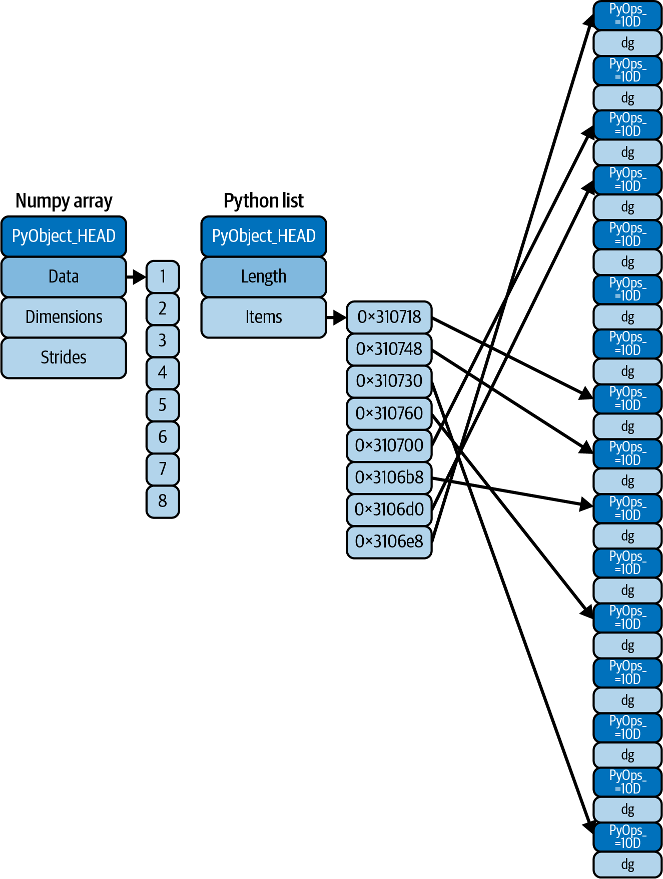
Fig. 8.1 Difference between NumPy array (C) and Python lists [Vanderplas, 2022]#
In short, NumPy’s primary data structure is the ndarray (N-dimensional array), which is a homogeneous, multidimensional array of fixed-size items. This means all elements within an ndarray must be of the same data type (note: To store heterogeneous data, NumPy uses structured arrays). While Python defines only one type of a particular data class (there is only one integer type, one floating-point type, etc.), there are 24 new fundamental Python types to describe different types of scalars in NumPy.
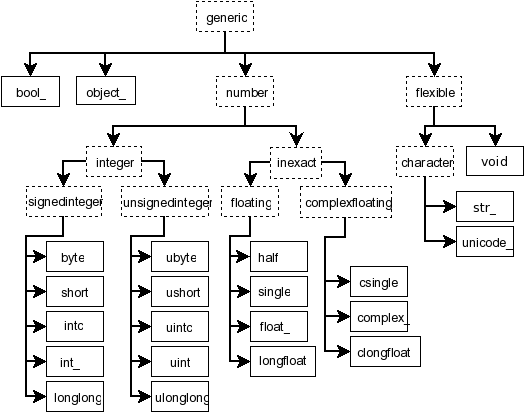
Fig. 8.2 Hierarchy of type objects representing the array data types (Numpy Scalars )#
Within the context of NumPy, the terms scalar, vector, and matrix refer to specific dimensions of these arrays.
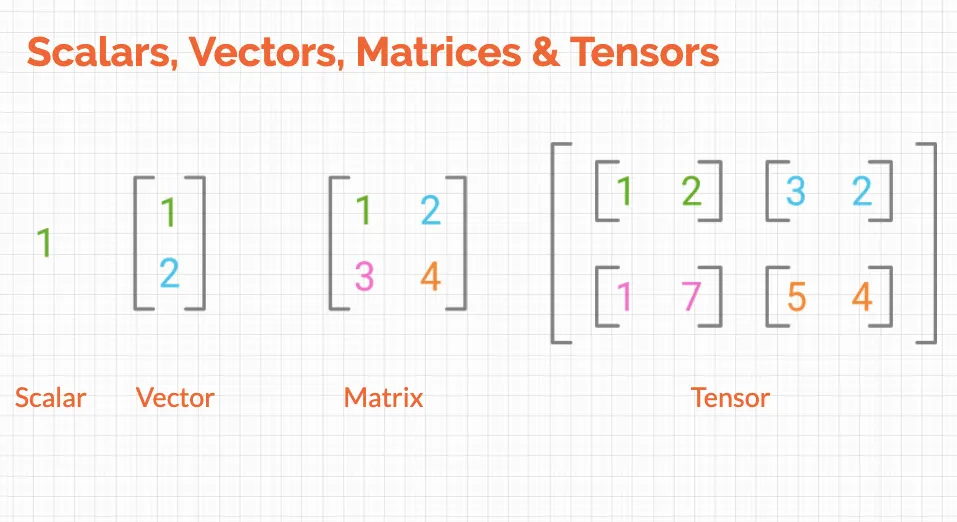
Fig. 8.3 Scalar, Vector, Mmatrix, and Tensor (Harshit Tyagi )#
8.1.1.2. Installing NumPy#
To install NumPy, you would:
go to command line
navigate to your project directory (dsm)
activate the virtual environment
issue the
pip install[package] syntax:
pip install numpy
You should see the installation happens like:
(.venv) tychen✪macː~/workspace/dsm$ pip install numpy
Collecting numpy
Downloading numpy-2.3.3-cp312-cp312-macosx_14_0_arm64.whl.metadata (62 kB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 62.1/62.1 kB 1.3 MB/s eta 0:00:00
Downloading numpy-2.3.3-cp312-cp312-macosx_14_0_arm64.whl (5.1 MB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 5.1/5.1 MB 4.1 MB/s eta 0:00:00
Installing collected packages: numpy
Successfully installed numpy-2.3.3
Note
Alternatively, in a Jupyter notebook, you may issue %pip install [package] in a code cell to install packages just like like pip install [package] in the command line. You will also see people use !pip install as well. !pip runs pip as a shell command, while %pip is a Jupyter magic function that works in the current running notebook kernel, which allows you to customize your notebooks.
Don’t forget to comment out your pip commands in the cells, or it will keep running every time you run the cells.
8.1.1.3. Using NumPy#
Once you’ve installed NumPy you can import it as a library:
import numpy as np
Numpy has many built-in functions and capabilities. For example:
arr = np.array([1, 2, 3, 4, 5]) ### creating array
print(np.mean(arr)) # mean
print(np.std(arr)) # standard deviation
Here we will focus on some of the most important aspects of Numpy:
vectors
arrays
matrices
number generation.
8.1.2. Creating NumPy Arrays#
8.1.2.1. From a Python List/Tuple#
You can create an array by directly casting a list to an array. Let us create a list first:
nums_list = [1,2,3, 4, 5]
nums_list
[1, 2, 3, 4, 5]
type(nums_list)
list
Now let’s cast the list into a numpy array using numpy’s array() method to create a 1-D array.
### before using numpy, import
### we usually import packages in the very beginning of a notebook
import numpy as np
arr = np.array(nums_list) ### casting a list to a numpy array
arr
### now you will see a numpy array, which is array([ ele, ele, ele ]) from the list [1, 2, 3, 4, 5]
array([1, 2, 3, 4, 5])
### data type is different from list too: numpy.ndarray
type(arr)
numpy.ndarray
We can also place the Python list directly into the np.array function to create a NumPy array (note that this is a 2-D array):
arr = np.array([[1, 2, 3],
[4, 5, 6]])
print(arr)
[[1 2 3]
[4 5 6]]
An example of Python 3-D “array” (list of lists):
list_of_list = [
[
[1, 2, 3, 4],
[2, 2, 3, 4],
[3, 2, 3, 4]
],
[
[4, 2, 3, 4],
[5, 2, 3, 4],
[6, 2, 3, 4]
]
]
list_of_list
[[[1, 2, 3, 4], [2, 2, 3, 4], [3, 2, 3, 4]],
[[4, 2, 3, 4], [5, 2, 3, 4], [6, 2, 3, 4]]]
Compare the result of evaluation of the Python list above with the NumPy array from the list:
np.array(list_of_list)
array([[[1, 2, 3, 4],
[2, 2, 3, 4],
[3, 2, 3, 4]],
[[4, 2, 3, 4],
[5, 2, 3, 4],
[6, 2, 3, 4]]])
8.1.2.1.1. Using List Comprehension#
Note the syntax of list comprehension is an alternative to for loops. Instead of initializing an empty list variable, running the for loop to append the elements, list comprehension is more concise.
import numpy as np
np.array([i**2 for i in range(10)])
array([ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81])
8.1.2.2. Using arange() Function#
numpy.arange() is a NumPy function used to create arrays with evenly spaced values with a specified interval. It is similar to Python’s built-in range() function, but returns a NumPy ndarray instead of a range object, which is more efficient for numerical operations.
np.arange(5)
array([0, 1, 2, 3, 4])
Using the range parameters: start, stop exclusive, stop:
np.arange(2, 11, 2)
array([ 2, 4, 6, 8, 10])
8.1.2.3. Using Other Functions:#
zeros()
ones()
full()
linspace()
eye
8.1.2.3.1. zeros(), ones(), and full()#
These functions initialize arrays of a specified shape filled with zeros, ones, or a constant value, respectively. The syntax for numpy.ones(), zeros(), and full() functions is:
numpy.ones(shape, dtype=None, order=’C’, *, like=None)
Note that we pass the shape argument using a list or a tuple or list.
np.ones(3)
array([1., 1., 1.])
np.ones([2,3], int) ### dtype is int
array([[1, 1, 1],
[1, 1, 1]])
np.zeros(5, dtype=int)
array([0, 0, 0, 0, 0])
np.zeros((5, 5)) ### by default dtype is float
array([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
np.full( (5) , 5)
array([5, 5, 5, 5, 5])
np.full((2, 3), 5) ### fill the shape (2x3) with 5
array([[5, 5, 5],
[5, 5, 5]])
8.1.2.3.2. linspace()#
linspace( ) stands for linear space. linspace returns evenly spaced numbers over a specified interval. Note that the stop parameter is inclusive.
### 11 numbers between 0 and 11, including 10
np.linspace(0, 10, 11, dtype=int)
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
arr = np.linspace(0, 26, 27)
print(arr)
print("shape :", arr.shape)
print("dimension: ", arr.ndim)
[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17.
18. 19. 20. 21. 22. 23. 24. 25. 26.]
shape : (27,)
dimension: 1
arr.reshape(3, 9)
array([[ 0., 1., 2., 3., 4., 5., 6., 7., 8.],
[ 9., 10., 11., 12., 13., 14., 15., 16., 17.],
[18., 19., 20., 21., 22., 23., 24., 25., 26.]])
8.1.2.3.3. eye()#
Creates an identity matrix
np.eye(4)
array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.]])
8.1.2.4. Using the numpy.random module#
(These functions are considered “legacy random generation ” and are for simple random data.
The numpy.random module in NumPy provides tools for generating pseudo-random numbers and sampling from various probability distributions. Some functions in the numpy.random module are commonly used:
np.random.rand(): returns random floating-point numbers (uniform distribution over the interval [0, 1))
np.random.randn(): returns random floating-point numbers (standard normal distribution with mean of 0 and standard deviation of 1)
np.random.randint(): returns random integers from a specified range
**np.rand
(note that np.random.random is the same as random.rand(), except random.random() takes the shape argument as a single tuple; e.g., see stackoverflow )
8.1.2.4.1. random.rand( )#
### rand: one number
np.random.rand()
0.6187251884687552
### rand: 1D array
from numpy import random ### different import syntax
random.rand(3)
array([0.81882214, 0.23120672, 0.25677838])
### rand: 2D
random.rand(2, 3)
array([[0.58031862, 0.22493981, 0.76087573],
[0.66546984, 0.14144829, 0.07164243]])
8.1.2.4.2. random.randn( )#
### randn: 1 number, normal distribution
np.random.randn()
-0.7466123025654965
### randn: 1D array
np.random.randn(5)
array([ 2.03722968, 0.8208662 , 1.16711514, -1.35818537, -0.54611995])
### randn: 2D array
np.random.randn(2, 3)
array([[-1.10953445, 0.24485299, 1.01145126],
[ 0.01749233, -0.21947827, 1.04604036]])
8.1.2.4.3. random.randint( )#
### randint: 1 number
print(random.randint(10)) ### range between 0 and 10 exclusive
print(random.randint(5, 10)) ### range between 5 and 10 exclusive
6
7
### randin: 1D array (with size parameter)
random.randint( 0, 10 ) ### 0 to 10 exclusie
4
8.1.2.4.4. choice( ) and size#
### the choice function
random.choice([3, 5, 7, 9], size = 2)
array([9, 9])
### the size parameter to generate N-D arrays
random.choice([3, 5, 7, 9], size=(3, 5))
array([[3, 3, 5, 9, 3],
[3, 9, 9, 5, 7],
[3, 9, 5, 7, 7]])
8.1.3. NumPy Indexing and Selection#
Just like Python lists, square brackets [] are used for selecting the elements or groups of elements from an array:
accessing individual elements of a list (indexing).
selecting sub-sequences (slicing with parameters: start, stop exclusive, and step). Note that slicing returns a numpy array.
negative indexing: begins with -1 from the end of the sequence.
import numpy as np
### creating sample array
arr = np.arange(0,10)
### show the array
arr
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
### indexing
arr[1]
np.int64(1)
arr[0:3]
array([0, 1, 2])
arr[0:5:2]
array([0, 2, 4])
arr[-1]
np.int64(9)
### start is -3, and stop is -1 exclusive
arr[-3:-1]
array([7, 8])
8.1.3.1. Indexing/Slicing 2-D Aarrays (Matrices)#
To access a 2-D array (matrices), use the syntax array[row_index, column_index]. The general format is arr[row][col] or arr[row, col].
### creating a 2-d array
arr_2d = np.array(([5,10,15],[20,25,30],[35,40,45]))
arr_2d
array([[ 5, 10, 15],
[20, 25, 30],
[35, 40, 45]])
### 0-based indexing; 1st row
arr_2d[0]
array([ 5, 10, 15])
### 0-based indexing
arr_2d[1, 2]
np.int64(30)
### 2D array slicing
### shape (2,2) from top right corner
arr_2d[:2, 1:]
array([[10, 15],
[25, 30]])
8.1.3.1.1. One More Example: 2-D Array (Matrices)#
arr_2d = np.array(([5,10,15],[20,25,30],[35,40,45]))
#Show
arr_2d
array([[ 5, 10, 15],
[20, 25, 30],
[35, 40, 45]])
### indexing row
arr_2d[1]
array([20, 25, 30])
### Format is arr_2d[row][col] or arr_2d[row,col]
### Getting individual element value
arr_2d[1][0]
np.int64(20)
### getting individual element value
arr_2d[1,0]
np.int64(20)
# 2D array slicing
### shape (2,2) from top right corner
arr_2d[:2,1:]
array([[10, 15],
[25, 30]])
### shape bottom row
arr_2d[2]
array([35, 40, 45])
### also shape bottom row with colon
arr_2d[2,:]
array([35, 40, 45])
8.1.4. NumPy Array Attributes#
Commonly used NumPy array attributes include:
ndim: number of dimensions (rank)shape: tuple of lengths per axis (assignable to reshape if sizes match)dtype: data type of elements (e.g., float64, int32, complex128)
8.1.4.1. dtype#
The dtype property in NumPy is an attribute of a NumPy array (ndarray) that represents the data type of the elements contained within the array.
You can get the data type of the object in the array:
arr = np.arange(25)
arr.dtype
dtype('int64')
arr_string = np.array(['apple', 'banana', 'cherry'])
print(arr_string.dtype)
### U means UTF8, 6 is the longest string
<U6
arr = np.array([1, 2, 3, 4], dtype='i4')
print(arr)
print(arr.dtype)
[1 2 3 4]
int32
8.1.4.2. ndim#
The ndim attribute represents the number of dimensions (or axes) of the array.
arr.ndim
1
arr_25 = np.arange(25)
arr_55 = arr_25.reshape(5, 5)
arr_55.ndim
2
8.1.4.3. shape#
The shape attribute returns a tuple of integers at every index tells about the number of elements the corresponding dimension has.
arr_2d = np.array([ [1, 2, 3], [4, 5, 6] ])
arr_2d.shape
(2, 3)
### create a 1-D array
arr_vec = np.arange(1, 10, 2)
arr_vec
array([1, 3, 5, 7, 9])
### a vector (an ordered list or an array of numbers, often
### representing multiple related variables or observations)
arr_vec.shape
(5,)
### np.array([list comprehension])
arr_25 = np.array([ num for num in range(25)])
arr_25
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24])
arr_25.shape
(25,)
8.1.4.4. The reshape() Function#
The reshape() function changes the shape of a NumPy array without altering its underlying data. It returns a new array (or a view of the original array if possible) with the specified new shape.
### arr
arr = np.array(
[num for num in range(16)]
)
arr
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15])
### reshape
arr = arr.reshape(4, 4)
arr
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
arr.reshape(2, 8)
array([[ 0, 1, 2, 3, 4, 5, 6, 7],
[ 8, 9, 10, 11, 12, 13, 14, 15]])
### this will not work
# arr.reshape(5,5)
arr_25 = np.arange(25)
arr_25.reshape(5, 5)
array([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24]])
arr_25.reshape(5, 5).shape
(5, 5)
### reshape does not change the object
arr_25
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22, 23, 24])
arr_25.shape
(25,)
